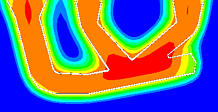
Temperaturverteilung nach 30 Zeiteinheiten
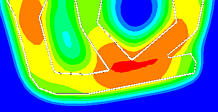
Temperaturverteilung nach 60 Zeiteinheiten

 Temperaturverteilung nach 30 Zeiteinheiten |
 Temperaturverteilung nach 60 Zeiteinheiten |
 |
| Abbildung 3: Temperaturverteilung über Kokille und Gußteil nach 30 bzw. 60 Zeiteinheiten |
 |
 |
 |