In Abschnitt 2.2 wurde dargestellt, daß der Gießprozeß
das zur Erstarrungssimulation verwendete FEM-Modell nicht eindeutig
vorschreibt und daß daher bei identischen
Anfangs- und Randbedingungen der Rechnung
sich im Rahmen einer vorgegebenen Genauigkeit
unterscheidende Temperaturverteilungen (aus verschiedenen
FEM-Modellen) die Erstarrung des Gußteils
gleichermaßen angemessen wiedergeben.
In ähnlicher Weise können auch für Kriteriumsfunktionen
aufgrund vieler
Zwischenschritte, die von den Simulationsergebnissen bis zur Bildung
von Qualitätszahlen durchlaufen werden, mehrere Varianten
gleichberechtigt nebeneinanderstehen.
Trotz einer festen Kombination von Eingangsparametern
streuen also - wie bei einem realen Versuch -
die Qualitätszahlen im Qualitätsvektor um einen ,,Mittelwert``. Als Beispiel sind in Tabelle 2
Qualitätszahlen für zwei verschiedene Vernetzungen
(Abbildung 8) aufgelistet,
wie sie sich mit den Anfangsbedingungen der
Simulation A (Abbildung 5) ergeben.
(Vernetzung I stimmt mit der bisher benutzten überein.)
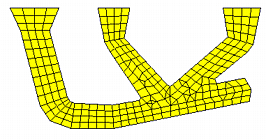
Vernetzung I des Gußteiles
|
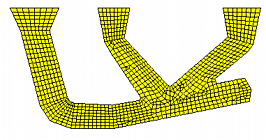
Vernetzung II des Gußteiles
|
Abbildung 8: Zwei verschiedene Vernetzungen des Gußteils
Tabelle 2 zeigt, daß bei
gleicher Gußteilqualität infolge unterschiedlicher mathematischer
Modellierungen der Qualitätsvektor nicht eindeutig bestimmt ist.
Um zu beurteilen, wann sich mit den Qualitätszahlen
auch tatsächlich die Gußteilqualität ändert, kann bei einer
vorgegebenen Irrtumswahrscheinlichkeit aus den ,,streuenden`` Qualitätsvektoren
für jede
Qualitätszahl Qi im Qualitätsvektor (i=1,...,6) eine untere Schranke Ui und eine obere Schranke Oi
für ein Toleranzintervall
berechnet werden.
Liegt Qi außerhalb des Toleranzintervalls (Qi < Ui oder Qi>Oi),
so hat sich die durch Qi beschriebene Gußteilqualität
mit einer statistischen Sicherheit von 1-a
signifikant
gegenüber der ursprünglichen Qualität geändert
(Ui und Oi wie in [14, S. 49]).
In Tabelle 2 sind
untere und obere Schranken aus dem Qualitätsvektor für Vernetzung I
und Vernetzung II des Gußteils mit
den Eingangsparametern der Simulation A bei einer statistischen
Sicherheit von 95% Irrtumswahrscheinlichkeit a=0.05) berechnet worden.
| Qualitätszahl |
Vernetzung I |
Vernetzung II |
Toleranzbereiche |
| untere Schranke |
obere Schranke |
| abs. Volumen |
0.026 |
0.018 |
0.000 |
0.048 |
| abs. Schrumpfung |
0.069 |
0.073 |
0.060 |
0.083 |
| rel. Schrumpfung |
0.210 |
0.240 |
0.130 |
0.321 |
| Monotonie Pfad 1 |
0.361 |
0.355 |
0.340 |
0.378 |
| Monotonie Pfad 2 |
0.545 |
0.539 |
0.522 |
0.563 |
| Monotonie Pfad 3 |
0.609 |
0.601 |
0.580 |
0.632 |
Tabelle 2: Qualitätszahlen und Toleranzbereiche (statistische Sicherheit 95%) für zwei verschiedene Vernetzungen des Gußteils mit den Eingangsparametern aus der Simulation A






